|
|
- zeros创建所有为0的矩阵
- ones创建所有为1的矩阵
- eye创建单位矩阵
- magic创建魔方矩阵
- rand随机产生均匀分布的矩阵0-1
- randn随机产生正态分布的矩阵
- randperm产生一个由指定整数元素随机分布构成的矩阵
- diag创建对角矩阵
- pascal创建PASCAL矩阵
>> zeros(4,4)ans = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0>> zeros(3)ans = 0 0 0 0 0 0 0 0 0>>
- ones创建所有为1的矩阵
>> ones(2,5)
ans =
1 1 1 1 1
1 1 1 1 1
>> ones(5)
ans =
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1 - eye创建单位矩阵
>> eye(4)ans = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1>>
>> magic(3)ans = 8 1 6 3 5 7 4 9 2
>> rand(10)ans = 0.6443 0.2077 0.3111 0.5949 0.0855 0.9631 0.0377 0.1068 0.0305 0.1829 0.3786 0.3012 0.9234 0.2622 0.2625 0.5468 0.8852 0.6538 0.7441 0.2399 0.8116 0.4709 0.4302 0.6028 0.8010 0.5211 0.9133 0.4942 0.5000 0.8865 0.5328 0.2305 0.1848 0.7112 0.0292 0.2316 0.7962 0.7791 0.4799 0.0287 0.3507 0.8443 0.9049 0.2217 0.9289 0.4889 0.0987 0.7150 0.9047 0.4899 0.9390 0.1948 0.9797 0.1174 0.7303 0.6241 0.2619 0.9037 0.6099 0.1679 0.8759 0.2259 0.4389 0.2967 0.4886 0.6791 0.3354 0.8909 0.6177 0.9787 0.5502 0.1707 0.1111 0.3188 0.5785 0.3955 0.6797 0.3342 0.8594 0.7127 0.6225 0.2277 0.2581 0.4242 0.2373 0.3674 0.1366 0.6987 0.8055 0.5005 0.5870 0.4357 0.4087 0.5079 0.4588 0.9880 0.7212 0.1978 0.5767 0.4711>> rand(1,1000);>> plot(ans)
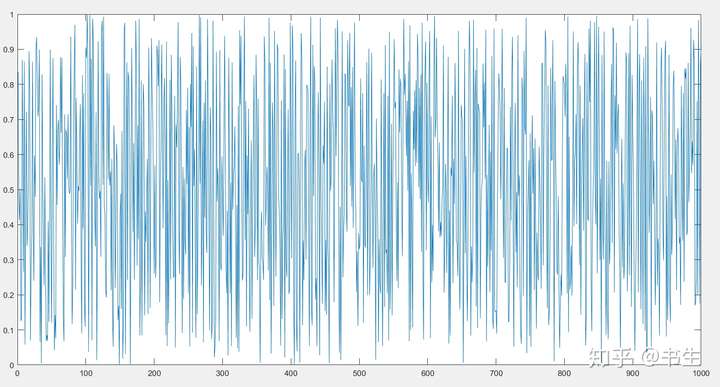 rand数据分布 rand数据分布
>> randn(10)ans = -0.2099 0.1097 0.8186 0.1093 -1.3270 1.5163 -1.1187 -0.7236 0.4128 -0.1980 -1.6989 1.1287 -0.2926 1.8140 -1.4410 -0.0326 -0.6264 -0.5933 -0.9870 0.3277 0.6076 -0.2900 -0.5408 0.3120 0.4018 1.6360 0.2495 0.4013 0.7596 -0.2383 -0.1178 1.2616 -0.3086 1.8045 1.4702 -0.4251 -0.9930 0.9421 -0.6572 0.2296 0.6992 0.4754 -1.0966 -0.7231 -0.3268 0.5894 0.9750 0.3005 -0.6039 0.4400 0.2696 1.1741 -0.4930 0.5265 0.8123 -0.0628 -0.6407 -0.3731 0.1769 -0.6169 0.4943 0.1269 -0.1807 -0.2603 0.5455 -2.0220 1.8089 0.8155 -0.3075 0.2748 -1.4831 -0.6568 0.0458 0.6001 -1.0516 -0.9821 -1.0799 0.7989 -0.1318 0.6011 -1.0203 -1.4814 -0.0638 0.5939 0.3975 0.6125 0.1992 0.1202 0.5954 0.0923 -0.4470 0.1555 0.6113 -2.1860 -0.7519 -0.0549 -1.5210 0.5712 1.0468 1.7298>> randn(1,1000);
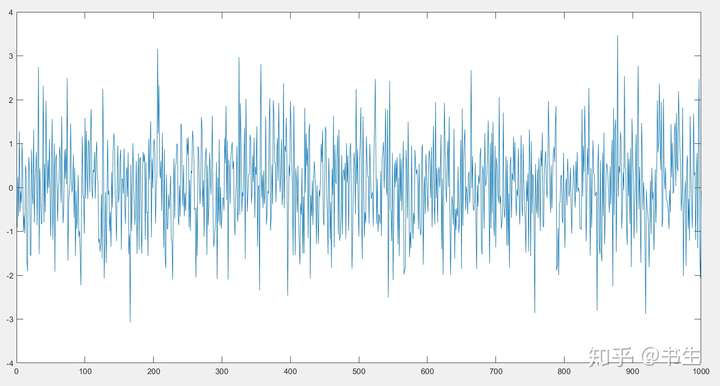 randn数据分布 randn数据分布
- randperm产生一个由指定整数元素随机分布构成的矩阵
>> randperm(100,10)ans = 16 97 94 48 77 14 40 86 73 88
>> v = [1 2 3 4];>> diag(v,-1)ans = 0 0 0 0 0 1 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 4 0>> diag(v,1)ans = 0 1 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 4 0 0 0 0 0>>
>> pascal(4)ans = 1 1 1 1 1 2 3 4 1 3 6 10 1 4 10 20>>
|
|
